Centripetal Force
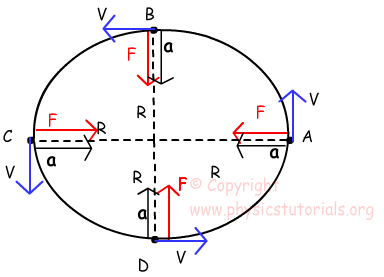
So far we have talked about angular speed, tangential speed and centripetal acceleration. As I mentioned in Newton’s Second Law of motion, if there is a net force than our mass has acceleration. In this case we find the acceleration first, so if there is acceleration then we can say there must be also a net force causing that acceleration. The direction of this net force is same as the direction of acceleration which is towards to the center. Look at the given picture that shows the directions of force and acceleration of an object doing circular motion in vertical. Don’t forget! Direction of acceleration and force is always same.
From the Newton’s Second Law of Motion;
F=m.a where; m is mass of the object, r is the radius of the circle,
Fc=-m4π²r/T² or T is the period, V is the tangential speed
Fc=mv²/r
Look at the given examples of centripetal force.
First picture shows the motion of a stone tied up with a string doing circular motion. T represents the tension of the string towards to the center. In this case centripetal force is equal to the tension in the rope. In second picture, a car has circular motion. Force exerted by the friction to the tiers of the car makes it do circular motion. Only force towards to the center is friction force. Thus, in this case our centripetal force becomes the friction force. We can increase the number of examples. For example, electrical forces or gravitational force towards to the center can be centripetal force of that system.
Example: Two objects A and B do circular motion with constant tangential speeds. Object A has mass 2m and radius R and object B has mass 3m and radius 2R. If the centripetal forces of these objects are the same find the ratio of the tangential speed of these objects.
Example: A car makes a turn on a curve of having radius 8m. If the car does not slide find the tangential velocity of it. (Coefficient of friction between the road and the tiers of the car =0,2 and g=10m/s²)
Circular Motion on Inclined Planes
We examine this subject with an example. Look at the given picture and analyze the forces shown on the picture.
As you can see from the picture given above, we showed the forces acting on the car. For having safe turn on the curve car must have the value given above which is the top limit. It can also have less speed than given above. If we want to increase the speed of the turn we should increase the slope of the road.
Example: Car having mass 1500kg makes a turn on the road having radius 150m and slope 20º. What is the maximum speed that car can have while turning for safe trip?
