Angular Velocity
Look at the given picture.
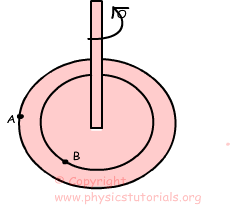If the platform does one rotation then points A and B also does one rotation. We define angular velocity as “change of the angular displacement in a unit of time”. the unit of angular velocity is revolution per unit time or radians per second. We show angular velocity with the Greek letter “ω” omega.
Average Velocity= Circumference of the Circle/Time
Average Speed/Velocity=2πr/T where, T is the period of the system and r is the radius of the revolution.
ω=2π/T=2πf where, f is frequency and T is the period Unlike tangential velocity, angular velocity of all points on the platform doing circular motion are equal to each other since the number of rotations per unit time are equal.
Example: If the stone does 6 rotations in 1 second find the angular velocity of it.
If the stone does four rotations in one second then its frequency becomes 6.
f=6s-¹
T=1/f=1/6s
ω=2π/T=2.3/1/6s=36radian/s