Vectors
Vectors, Additon of Vectors and Components of Vectors
In physics and all science branches quantities are categorized in two ways. Scalars and vectors are used for to define quantities. We can use scalars in just indication of the magnitude, they are only numerical value of that quantity. However, if we talk about the vectors we should consider more than numeric value of the quantities. Vectors are explained in detail below.
Vectors
Vectors are used for some quantities having both magnitude and direction. We will first learn the properties of vectors and then pass to the vector quantities. You will be more familiar with concepts after learning vectors. Look at the given shape which is a vector having magnitude and direction.
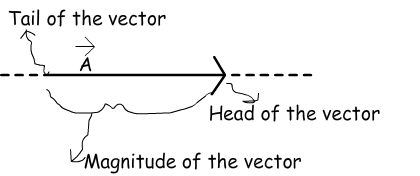We can change the position of the vector however, we should be careful not to change the direction and magnitude of it. In next subject we will learn how to add and subtract vectors. Moreover, we will learn how to find the X and Y components of a given vector using a little bit trigonometry.
Addition of Vectors
Look at the picture given below. It shows the classical addition of three vectors. We can add them just like they are scalars. However, you should be careful, they are not scalar quantities. They have both magnitude and direction. In this example their magnitudes and directions are the same thus; we just add them and write the resultant vector.
Let’s look at a different example.In this example as you can see the vector A has negative direction with respect to vectors B and C. So, while we add them we should consider their directions and we put a minus sign before the vector A. As a result our resultant vector becomes smaller in magnitude than the first example.
Multiplying a Vector with a Scalar
When we multiply a vector with a scalar quantity, if the scalar is positive than we just multiply the scalar with the magnitude of the vector. But, if the scalar is negative then we must change the direction of the vector. Example given below shows the details of multiplication of vectors with scalar.
Example: Find 2A, -2A and 1/2A from the given vector A.
Components of Vectors
Vectors are not given all the time in the four directions. For doing calculation more simple sometimes we need to show vectors as in the X, -X and Y, -Y components.
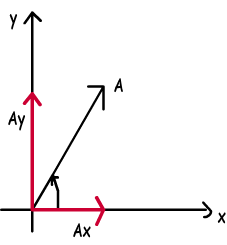For example, look at the given vector above, it is in northeast direction. In the figure, we see the X and Y component of this vector. In other words, addition of Ax and Ay gives us A vector. We benefit from trigonometry at this point. I will give two simple equations which you can use and find the components of any given vector.
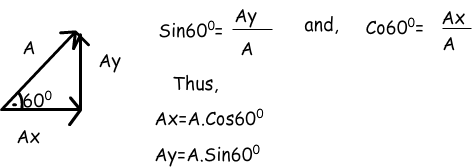All vectors can be divided into their components. Now we solve an example and see how we use this technique.
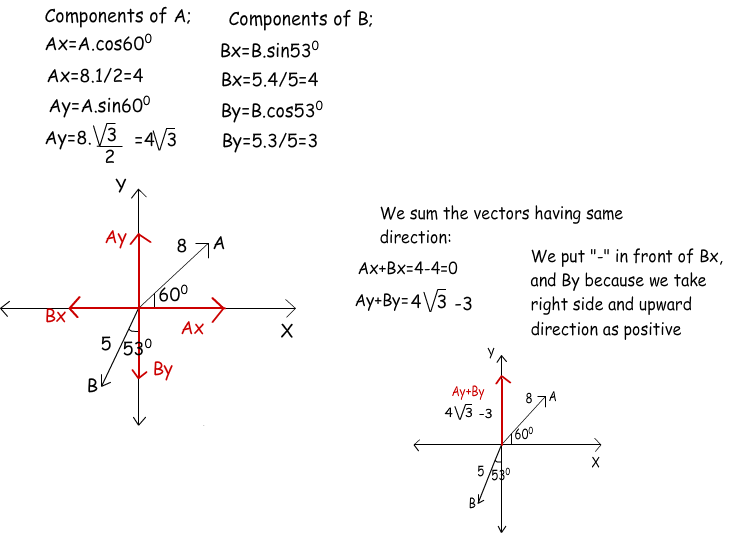
Example: Find the resultant vector of A and B given in the graph below. (sin30º=1/2, sin60º=√3/2, sin53º=4/5, cos53º=3/5)
We use trigonometric equations first and find the components of the vectors then, make addition and subtraction between the vectors sharing same direction.
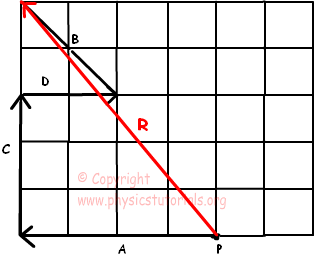
Example: Find resultant of the following forces acting on an object at point P in figure given below.
We add all vectros to find resultant force. Start with vector A and add vector C to it. After that, add vector D and C and draw resultant vector by the starting point to the end. Examine given solution below, resultant force is given in red color.
