Free Fall
Free Fall with Examples
Free fall is a kind of motion that everybody can observe in daily life. We drop something accidentally or purposely and see its motion. At the beginning it has low speed and until the end it gains speed and before the crash it reaches its maximum speed.
Which factors affect the speed of the object while it is in free fall? How can we calculate the distance it takes, time it takes during the free fall? We deal with these subjects in this section. First, let me begin with the source of increasing in the amount of speed during the fall. As you can guess, things fall because of the gravity. Thus, our objects gain speed approximately10m/s in a second while falling because of the gravitation. We call this acceleration in physics gravitational acceleration and show with “g”. The value of g is 9,8m/s² however, in our examples we assume it 10 m/ s² for simple calculations. Now it’s time to formulize what we said above. We talked about the increase in speed which is equal to the amount of g in a second. Thus our velocity can be found by the formula;
V=g.t
where g is gravitational acceleration and t is the time.
Look at the given example below and try to understand what I tried to explain above.
Example: The boy drops the ball from a roof of the house which takes 3 seconds to hit the ground. Calculate the velocity before the ball crashes to the ground. (g=10m/s²)
Velocity is;
V=g.t
V=10m/ s².3s=30m/s
We have learned how to find the velocity of the object at a given time. Now we will learn how to find the distance taken during the motion. I give some equations to calculate distance and other quantities. Galileo found an equation for distance from his experiments.
This equation is;
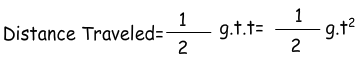Using this equation we can find the height of the house in given example above. Let’s found how height the ball has been dropped? We use 10 m/s² for g.
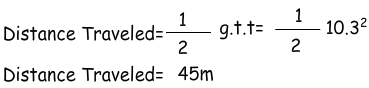I think the formula now a little bit clearer in your mind. We will solve more problems related to this topic. Now, think that if I throw the ball straight upward with an initial velocity. When it stops and falls back to the ground? We answer these questions now.
Picture given above shows the magnitudes of velocity at the bottom and at the top. As you can see the ball is thrown upward with an initial v velocity, at the top it’s velocity becomes zero and it changes it’s direction and starts to fall down which is free fall. Finally at the bottom before the crash it reaches its maximum speed which shown as V’. We have talked about the amount of increase in the velocity in free fall. It increases 9,8m/s in each second due to the gravitational acceleration. In this case, there is also g but the ball’s direction is upward; so the sign of g is negative. Thus, our velocity decreases in 9,8m/s in each second until the velocity becomes zero. At the top, because of the zero velocity, the ball changes its direction and starts to free fall. Before solving problems I want to give the graphs of free fall motion.
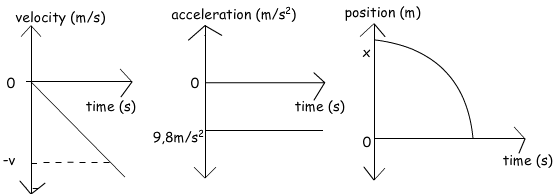As you see in the graphs our velocity is linearly increases with an acceleration “g”, second graphs tells us that acceleration is constant at 9,8m/s², and finally third graphic is the representation of change in our position. At the beginning we have a positive displacement and as the time passes it decreases and finally becomes zero. Now we can solve problems using these graphs and explanations.
Example: John throws the ball straight upward and after 1 second it reaches its maximum height then it does free fall motion which takes 2 seconds. Calculate the maximum height and velocity of the ball before it crashes the ground. (g=10m/s²)
Example: An object does free fall motion. It hits the ground after 4 seconds. Calculate the velocity of the object after 3 seconds and before it hits the ground. What can be the height it is thrown?
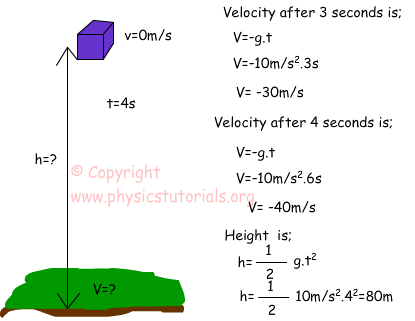Two examples given above try to show how to use free fall equations. We can find the velocity, distance and time from the given data. Now, I will give three more equations and finishes 1D Kinematics subject. The equations are;
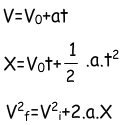First equation is used for finding the velocity of the object having initial velocity and acceleration. Second one is used for calculating the distance of the object having initial velocity and acceleration. Third and last equation is timeless velocity equation. If distance, initial velocity and acceleration of the object is known then you can find the final velocity of the object. Now let’s solve some problems using these equations to comprehend the subject in detail.
Example: Calculate the velocity of the car which has initial velocity 24m/s and acceleration 3m/s² after 15 second.
We use the first equation to solve this question.
Example: The car which is initially at rest has an acceleration 7m/s² and travels 20 seconds. Find the distance it covers during this period.
