Friction Force
Friction force results from the interactions of surfaces. Irregularities in the structure of the matters causes friction force. These irregularities can be detected in micro dimensions. You may not see any irregularity on the surface of the material however, it does exist. Friction force is always opposite to the direction of motion and tends to decrease net force. All materials have their own friction constant in other words friction force depends on the type of materials. Another factor affecting friction force is the normal force. When you apply a force to an object, then friction force becomes active and resists with the force of having opposite direction to your net force.
We can calculate the friction force by this formula;
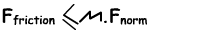Where, µ is the coefficient of friction and it depends on the type of material. Fnorm is the reaction of the surface to the object because of its weight.
Ffriction≤ µ.m.g We assume that weight as m.g, however if the object is on an inclined plane than we take the vertical component of the mass while calculating weight.
Friction can be studied under two topics static friction and sliding friction. Surfaces apply different friction constant when the object is at rest and sliding. Interestingly, the friction constant of the objects at rest is higher than the friction constant of the sliding objects. The sliding friction force is calculated by using the µ and the Fnorm normal force that surface apply to the object.
Ffriction= µsliding.m.g sliding
Friction force also exists when there is no motion. If two objects are in contact then we can talk about friction force there is no need for motion. In static friction force, two objects are in contact however there is no motion in other words object does not slide on the surface. You all experience the static friction in daily life. For example, suppose that you push a huge box, which is on the carpet, however, box does not move. Static friction becomes exist when you apply a force to the object. The amount of the static friction is equal to the amount hat you apply and the direction is opposite to the direction of the motion. If you increase the applied force until one point static friction also increases. We will calculate this limit point by the formula given below.
Ffriction = µstatic.m.g static
We use ≤ symbol instead of =, because static friction changes with respect to the applied force. It has the value of 1 to the limit value. We calculate the limit value by the formula given above. Most of the time magnitude of static friction is greater than magnitude of sliding friction for same surfaces. We solve some problems related to the friction and Newton’s law of motions.
Example: 50N of force is applied to the 6 kg box. If the coefficient of friction is 0,3, find the acceleration of the box.
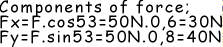Free body diagram of the system is given above. From this diagram we find the normal force of the surface and friction force.
Fnormal=mg-Fy
Fnormal =60N-40N=20N
And friction force is;
Ffriction=µ.Fnormal=0,3.20N=6N
Net force in –Y to Y is zero, in other words box is in equilibrium in this direction. However, in –X +X direction net force is not zero so there is a motion and acceleration in this direction.
Fnet=m.a
Fx-Ffriction=m.a
30N-6N=6kg.a
a=4m/s²
Example: Find the acceleration of the system. (µ=0,4, sin37º=0,6, cos37º=0,8 and g=10m/s²)
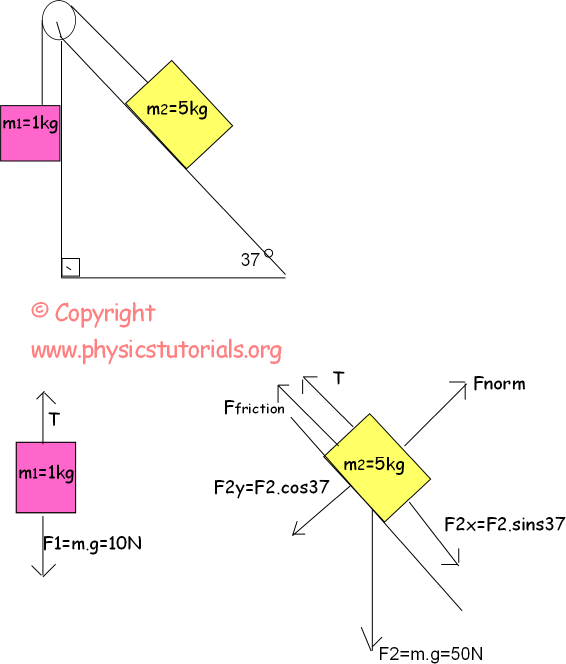Fnet=m.a
F2x - Ffriction - T = m.a
F2.sin37º - µ.F2.cos37º - 10 = (5kg + 1kg).a
(50.0,6) - (0,4.50.0,8) - 10 = 6.a
30 - 16 - 10 = 6.a
a = 0.66 m/s²