Magnetism Cheat Sheet
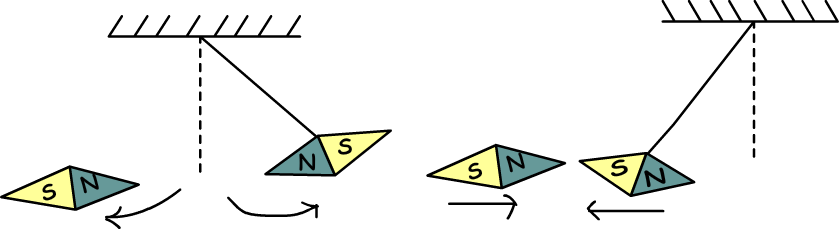
Magnets exists always in dipoles North Pole (represented by N) and South Pole (represented by S). If you break the rock into pieces you get small magnets and each magnet also has two poles N and S.
Same poles of the magnet like in the electricity repel each other and opposite poles attract each other.
Coulomb’s Law for Magnetism
Magnets exert force to each other.
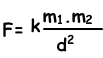F₁=-F₂
Where; k is the constant, m₁ and m₂ are the magnetic intensities of the poles and d is the distance between them.
Magnetic Field
Magnets show repulsion or attraction force around itself. This area affected from the force of magnets called magnetic field. Direction of the magnetic field lines shown below;
Magnetic field lines around a wire are shown below;
Magnetic field is a vector quantity and showed with the letter B. Unit of B is Tesla. When we calculate magnetic field of a magnet we assume that there is a 1 unit of m at the point we want to find. We find the magnetic field with following formula;
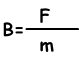Magnetic Flux
Magnetic flux is the number of magnetic field lines passing through a surface placed in a magnetic field.
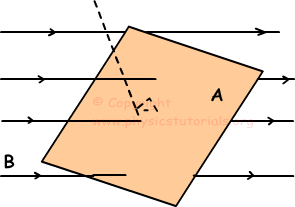We show magnetic flux with the Greek letter; Ф. We find it with following formula;
Ф=B.A.cosӨ
Where Ф is the magnetic flux and unit of Ф is Weber (Wb)
B is the magnetic field and unit of B is Tesla
A is the area of the surface and unit of A is m²
Magnetic Permeability
Diamagnetic matters: If the relative permeability f the matter is a little bit lower than 1 then we say these matters are diamagnetic.
Paramagnetic matters: If the relative permeability of the matter is a little bit higher than 1 then we say these matters are paramagnetic.
Ferromagnetic matters: If the relative permeability of the matter is higher than 1 with respect to paramagnetic matters then we say these matters are ferromagnetic matters.
Magnetic Effect of Current
If you move the magnet placed near the circuit you produce current or, if you change the current of circuit you can get current in another circuit placed near it.
Magnetic Field around a Wire
Current flowing in a linear wire produces magnetic field B=2k.i/d at a distance d.
We show the current in two ways, if the current towards to us we show it with a dot, if the current is outward we show it with cross.
Magnetic Field around a Circular Wire
Circular wire produces magnetic field inside the circle and outside the circle. Magnetic field around a circular wire is calculated by the formula;
B=2πk.i/r
Magnetic Field around a Solenoid
Picture given below shows the solenoid. A typical solenoid behaves like a bar magnet. Magnetic field produced by solenoid is constant inside the solenoid and parallel to the axis of it.
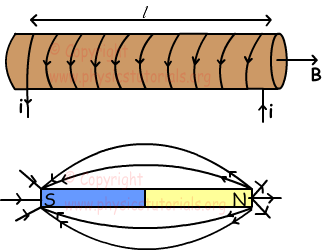We find the magnetic field produced by solenoid with the following formula;
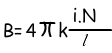Where: i is the current, N is the number of loops and l is the length of the solenoid.
Force Acting on Moving Particle and Current Carrying Wire
Experiments done on this subject show that we can find the force exerted on the current carrying wire with following formula;
F=B.i.l.sinß
We find direction of the force by right hand rule. Picture given below shows the direction of magnetic field current and force;
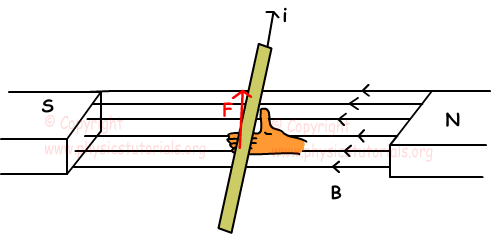Force Acting on Charged Particle
If the particle has charge q, velocity v and it is placed in a magnetic field having strength B force acting on this particle and ß is the agle between the velocity and magnetic field is found with following formula;
F=q.v.B.sinß
Forces of Currents Carrying Wires on Each Other
Experiments done on this subject shows that currents in the same direction attract each other since they produce opposite magnetic fields. On the contrary currents in opposite directions repel each other since they produce magnetic fields having same directions. We find the force exerted on each of them with following formula,
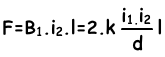Where; l is the length of the wires, d is the distance between them.