Rotational Motion Exam 2 and Problem Solutions

1. An object in horizontal rotates on a circular road with 10m/s velocity. It does 120 revolutions in one minute.

a) Find frequency and period of the object.

b) Find the change in velocity vector when it rotates 60⁰, 90⁰ and 180⁰.

a) 60s.f=120 revolution

f=2 revolution/second

T=1/f=1/2s

b) Rotational Motion If object starts its motion from point A and rotates 60⁰ and comes point B;

ΔV=VB-VA Rotational Motion ΔV=2V.cos120⁰/2=2.10.cos60⁰=20/2=10m/s

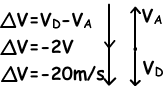
If object rotates 90⁰; Rotational Motion If object rotates 180⁰; Rotational Motion 2. A device does 1800 revolution in 6 minutes. Find angular velocity and period of this device. (π=3)

1800.T=6.60s

T=360/1800=1/5s

ω=2π/T=2.3/1/5=30 radian/s

3. Friction constant of a circular road, having radius 50m, is 0,2. Find the initial velocity of the car having 1500 kg to turn junction safely. Rotational Motion Ffriction≥Fcentripetal (for safe turn)

k.m.g≥m.V²/r

k.g.r≥V²

100≥V²

10m/s≥V or

36km/h≥V

4. A marble is thrown with velocity V from point A. If no force is exerted on surface by marble at point B, find the force exerted on point A by marble. (Assume that velocity of marble is constant.) Rotational Motion Since no force is exerted on point B by marble;

mg=mV²/R

V²=g.R Rotational Motion Force exerted by marble on point A;

FA=G+F

FA=mg+mV²/R (we put V²=gR into the equation)

FA=mg+mgR/R

FA=2mg

5. Two objects rotate with same frequency around point O. One of the objects has mass m and other one has mass 9m. If centripetal forces exerted on objects having mass m is F₁, and object having mass 9m is F₂, find ratio of F₁/F₂. Rotational Motion V₁=2.π.r.f

V₂=2.π.3r.f

V₂=3V₁

F₁/F₂=mV₁²/r/9mV₂²/3r=V₁²/r.3r/9V₂²

F₁/F₂=1/27