Heat Temperature and Thermal Expansion Exam 1 and Problem Solutions

1. Two thermometer X shows boiling point of water 220X and freezing point of water 20X and Y shows boiling point of water 120 Y and freezing point of water -40Y. If thermometer X shows 100X, find the value that thermometer Y shows. (X-20)/200=(Y-(-40))/160

(X-20)/20=(Y+40)/16

Y=24⁰Y

2. Two matters have specific heat capacities c and 2c. If we give Q and 4Q heat to these matters, changes in the temperatures of them become equal. If the matter A has mass m, find the mass of matter B in terms of m.

Heat gained, lost by the matters is found with following formula;

Q=m.c.ΔT

Heat gained by A and B;

Q=mA.c.ΔT

4Q=mB.2c.ΔT

mB=2mA

mB=2m

3. A and B matters have equal masses. Find the ratio of cA/cB. Q=m.c.ΔT

30=m.cA.(10-0)

30=m.cB(20-0)

cA/cB=2

4. Table given above shows initial lengths, changes in temperatures and changes in the length of 3 rods. Find whether these rods are made of same matters or not.

ΔL=L₀.α.ΔT

αA=ΔL/2L.ΔT

αB=3.ΔL/3L.2ΔT

αC=ΔL/4L.ΔT

αA=αB>αC

Thus, A and B can be same matter but C is different from them.

5. Three cylinders made of same matter and at same temperature, are placed on a platform. Same amount of heat given to the cylinders make same amount of change in their temperature. Find the relation between changes in the lengths of these cylinders. 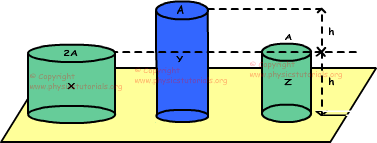If we say volume of X is V, then volume of Y is also V and Z is V/2. There is a linear relation between volumes and mass, we use this relation in solution of the problem.

Q=m.c.ΔTX, ΔTX=T

Q=m.c.ΔTY, ΔTY=T

Q=m/2.c.ΔTZ, ΔTZ=2T

Changes in the lengths of cylinders;

ΔLX=h.α.T=ΔL

ΔLY=2h.α.T=2ΔL

ΔLZ=h.α.2T=2ΔL

ΔLY=ΔLZ>ΔLX