Electrostatics Exam 2 and Problem Solutions

1. Find the equivalent capacitance between points A and B. If we redraw circuit given above; 1/Ceq₁=1/2C+1/2C

Ceq₁=1C

1/Ceq₂=1/4C+1/4C

Ceq₂=2C

CAB=1C+2C+2C=5C

2. Find relation between the electrical energies stored in the capacitors. Since capacitors are connected in parallels, potentials in each branch are equal.

W₁=1/2.6C.22=12C

W₂=1/2.3C.42=24C

W₃=1/2.3C.62=54C

W₃ >W₂ >W₁

3. Neutral sphere A, positively charged sphere B and negatively charged sphere C are given below. If we touch B inside of the A and C to outside of the A, find the final charges of spheres. When we touch B inside of A, all charges of B are transferred to A and B becomes neutral. When we touch C outside of A, it is positively charged. Final charges of spheres;

A: is positively charged

B: is neutral

C: is positively charged

4. A and B produce potential V at point X. If total potential at point X is -V, find qC. VAB=k.q/d+k.2q/d=3k.q/d=V

VX=3k.q/d+k.qC/d=-V

3k.q/d+k.qC/d=-3k.q/d

qC=-6q

5. If the capacitance of first capacitor is C, find the capacitance of second capacitor. 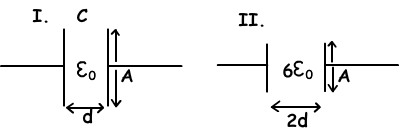C₁=ε₀.A/d=C

C₂=6ε₀.A/2/2d=6/4ε₀.A/d=3/2C