Vectores
Vectores Suma De Vectores Componentes De Vectores Con Ejemplos
En la física y todas las cantidades de la ciencia ramas se clasifican de dos maneras. Escalares y vectorsare utilizado para definir las cantidades. Podemos utilizar los escalares en sólo indicio de la magnitud, son sólo el valor numérico de esta cantidad. Sin embargo, si hablamos de los vectores que debemos considerar más que el valor numérico de las cantidades. Vectores se explican en detalle a continuación.
Vectores
Vectores se usan para algunas cantidades que tiene magnitud y dirección. En primer lugar, se aprenden las propiedades de los vectores y luego pasar a las cantidades vectoriales. Usted estará más familiarizado con los conceptos después de vectores de aprendizaje. Mira la forma determinada que es un vector que tiene magnitud y dirección.
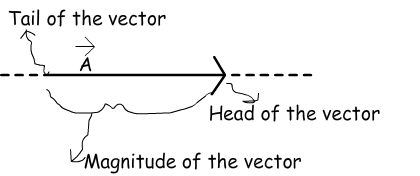Jefe de thevector muestra la dirección y la cola se muestra el punto de partida. Podemos cambiar la posición del vector sin embargo, debemos tener cuidado de no cambiar la dirección y la magnitud de la misma. En siguiente tema vamos a aprender a sumar y restar vectores. Por otra parte, vamos a aprender cómo encontrar los componentes X e Y de un vector dado con un poco de trigonometría.
Suma de Vectores
Mira la foto a continuación. Se muestra la adición clásica de tres vectores. Podemos añadir al igual que lo son escalares. Sin embargo, usted debe tener cuidado, no son cantidades escalares. Ellos tienen magnitud y dirección. En este ejemplo, sus magnitudes y las direcciones son las mismas por lo tanto, que hay que añadirlas y escribir el vector resultante.
Echemos un vistazo a un example.In diferentes este ejemplo como se puede ver el vector A tiene una dirección negativa con respecto a los vectores B y C. Por lo tanto, mientras que los añadimos que debemos considerar sus direcciones y poner un signo menos delante del vector A. como resultado, nuestro vector resultante se hace más pequeño en magnitud que el primer ejemplo.
La multiplicación de un vector con un escalar
Cuando multiplicamos un vector con una magnitud escalar, si el escalar es positivo que acabamos de multiplicar el escalar con la magnitud del vector. Pero, si el escalar es negativo, entonces tenemos que cambiar la dirección del vector. Ejemplo A continuación se muestran los detalles de la multiplicación de los vectores con escalares.
Ejemplo: Encontrar 2A-2A y 1/2A del vector dado A.
Componentes de los Vectores
Vectores no se les da todo el tiempo en las cuatro direcciones. Para hacer el cálculo más simple a veces tenemos que demostrar vectores como en el X, X e Y, Y-componentes.
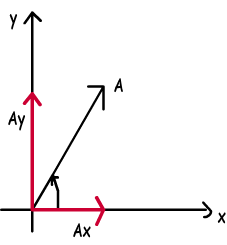Por ejemplo, mire el vector a continuación, es en dirección noreste. En la figura, vemos que el componente X y Y de este vector. En otras palabras, la adición de Ax y Ay nos da un vector. Nos beneficiamos de la trigonometría en este momento. Voy a dar dos ecuaciones simples que se pueden utilizar y encontrar los componentes de cualquier vector dado.
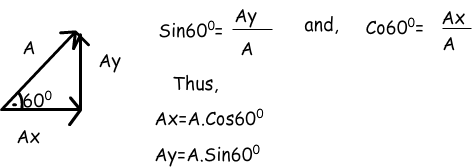Todos los vectores se puede dividir en sus componentes. Ahora resolvemos un ejemplo y ver cómo podemos utilizar esta técnica.
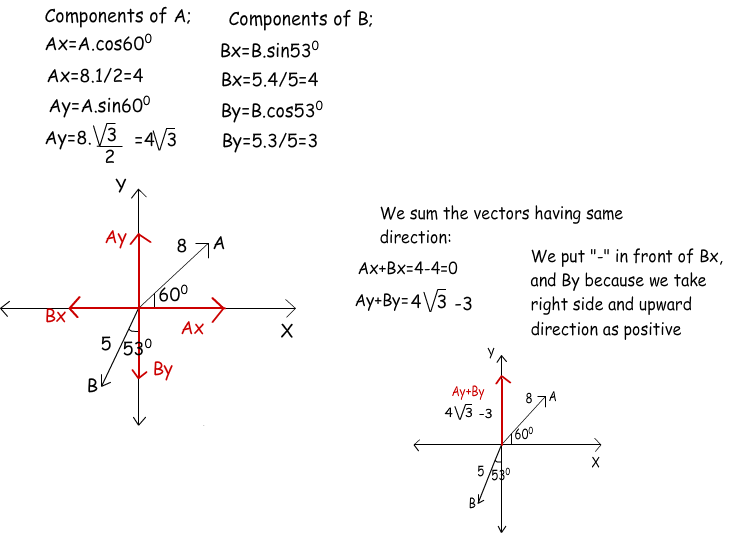
Ejemplo: Encontrar el vector resultante de A y B que figuran en el gráfico siguiente.(sin30º=1/2, sin60º=√3/2, sin53º=4/5, cos53º=3/5)
Primero usamos ecuaciones trigonométricas y encontramos los componentes de los vectores, luego hacemos sumas y restas entre los vectores que comparten la misma dirección.
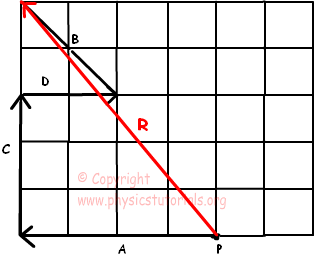
Ejemplo: Encontrar resultante de las siguientes fuerzas actúan sobre un objeto en el punto P en la figura a continuación.
Sumamos todos los vectros para encontrar la fuerza resultante. Comience con un vector y agregar vector C a la misma. Después de eso, añadir vectores D y C y dibujar vector resultante por el punto de partida hasta el final. Examine la solución dada a continuación, la fuerza resultante se presenta en color rojo.
