Interferencia de las Ondas de Primavera
Velocidad de las ondas periódicas
Hemos aprendido que, si el medio es constante de velocidad de la onda también es constante y nos dio las siguientes ecuaciones para la velocidad de las ondas;
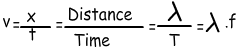
Ejemplo: Encontrar la relación de longitudes de onda de las ondas dada.
Se define la longitud de onda como la distancia entre las crestas secuencial o troughs.Picture a continuación muestra las longitudes de onda de cada onda y la relación entre ellos.
Ejemplo: El uso de los datos que figuran en la siguiente imagen, encontrar la longitud de onda, la velocidad y la amplitud de la onda. Frecuencia de la fuente es 2s⁻¹ .
Nos encontramos con la longitud de onda de la onda de la imagen como;
8m
Nos encontramos con la velocidad de la onda usando la siguiente fórmula;
v= longitud de onda. freguency=8m.2s-1=16m/s
Amplitud de la onda es de 2m de la imagen dada.
Interferencia de las ondas de Primavera
Cuando las ondas interfieren dos que producen onda resultante. En esta sección aprenderá a encontrar la onda resultante. El desplazamiento de la onda resultante es la suma de las olas que lo produce. Mira las fotos a continuación. Que muestran el comportamiento de las olas antes de la intervención, y después de la interferencia.
Ejemplo: Las amplitudes de las ondas se indican a continuación son A₁ y A₂. La imagen muestra la interferencia de dos ondas.
Cuadro que se presenta a continuación muestra dos ondas idénticas interferencia con direcciones opuestas.
¡Ten cuidado!
Si las amplitudes de las ondas con direcciones opuestas son diferentes, entonces la amplitud de la onda resultante se convierte en la diferencia de las amplitudes de las ondas. Tiene la misma dirección con la ola más grande.