La Rapidez Tangencial De Velocidad
Rapidez lineal (rapidez tangencial):
Rapidez lineal y rapidez tangencial da el mismo significado para el movimiento circular. En movimiento una dimensión que define la rapidez como la distancia tomada en una unidad de tiempo. En este caso utilizamos la definición misma de nuevo. Sin embargo, en este caso la dirección del movimiento es siempre tangente a la trayectoria del objeto. Por lo tanto, también se puede llamar como la rapidez tangencial, la distancia tomada en un momento dado. Mira la foto que da y tratar de secuencia de las velocidades de los puntos de mayor a menor.
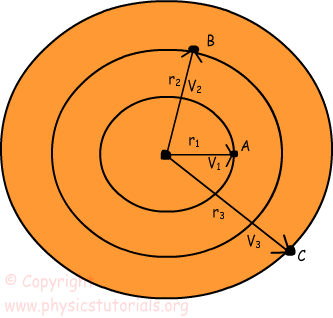
En un período de tiempo determinado todos los puntos de este objeto en rotación han mismas revoluciones. En otras palabras, si A completa una revolución, entonces B y C también tienen una revolución en un mismo tiempo. La fórmula de la rapidez en el movimiento lineal;
rapidez = distancia / tiempo
Como he dicho antes, la rapidez en el movimiento circular también se define como la distancia tomada en un momento dado. Por lo tanto, las rapidez de los puntos dados en la siguiente imagen se;
V = distancia / tiempo Si el objeto tiene una vuelta completa a continuación, la distancia recorrida se hace; 2πr que es la circunferencia de un círculo el objeto.
VA=2πr/tiempo
Período: El paso del tiempo para una revolución que se llama periodo. La unidad del periodo es el segundo. T es la representación de la época.
La ecuación de la rapidez tangencial se vuelve;
VA=2πr/T
Frecuencia: Número de revoluciones por segundo. La unidad de frecuencia es 1/segundo. Se muestra la frecuencia con la letra f.
La relación de f y T;
f=1/T
Ahora, con la ayuda de la información anterior secuencia permite “las velocidades de los puntos en la imagen dada.
Puesto que la velocidad o la rapidez de los puntos de objeto en rotación es linealmente proporcional a la radio r3>r2>r1;
V3>V2>V1 TEn resumen, podemos decir que la rapidez tangencial del objeto es directamente proporcional a la distancia desde el centro. Aumento en los resultados de la distancia en el aumento de la cantidad de rapidez. A medida que avanzamos en el centro disminuye la rapidez, y en el centro de la rapidez se convierte en cero. Nosotros usamos la misma unidad de la rapidez tangencial de movimiento lineal que es “m / s”.
Ejemplo: Una partícula con masa m viaja del punto A al B en una trayectoria circular con radio R en 4 segundos. Determinar el periodo de esta partícula.
Partícula viaja de un cuarto de círculo en 4 segundos. El período es el tiempo necesario para una revolución. Por lo tanto,
T/4=4s
T=16s.
Ejemplo: Si la partícula tiene masa m viaja del punto A al B en 4 segundos encontrar la velocidad tangencial de la partícula dada en la imagen a continuación. (π=3)
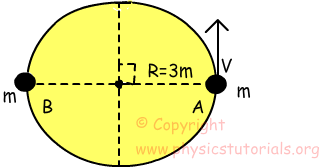En primer lugar, encontrar el período del movimiento. Si la partícula recorre la mitad del círculo en 4 segundos;
T/2=4s
T=8s
v=2 π R/T
v=2.3.3m/8s=9/4 m/s rapidez tangencial de la partícula