Trabajo, Poder Y Energía Examen 3 Y Soluciones

1. Una caja se libera desde el punto A y pasa desde el punto D, con una velocidad V. Las obras hechas por la gravedad son W₁ entre AB, W₂ y W₃ entre BC entre CD. Encontrar la relación entre ellos. El trabajo realizado por la gravedad es igual al cambio en la energía potencial del objeto.

intervalo AB: W₁=ΔEp=-mgh

intervalo BC: W₂=ΔEp=-mgh

intervalo CD: W₃=ΔEp=0

W₁=W₂>W₃

2. Un objeto lanzado con una velocidad inicial V desde el punto A. Se alcanza el punto B y se vuelve al punto A y se detiene. Encontrar la relación entre el objeto tiene energía cinética en el punto A y la energía que se pierde en la fricción. Objeto tiene energía cinética en el punto A;

EK=1/2.mV²

Objeto se detiene en el punto A, lo que significa que toda la energía se pierde en la fricción.

EK=Efriction

3. Lanzamos objeto desde un punto A con una energía cinética E inicial, y se llega al punto C. ¿Cuánta energía se debe dar para hacer punto del objeto llegar a D. Usando el teorema de conservación de la energía;

E=2mgh+Ffriction.2X

E=2(mgh+Ffriction.X)

mgh+Ffriction.X=E/2

E’=3mgh+Ffriction.3X

E’=3(mgh+Ffriction.X)

E’=3.E/2=1,5E

tenemos que dar 1,5E de la energía para hacer punto del objeto llegar a D.

4. Tres placas rectangulares son ahorcados, como se muestra en la figura a continuación. Si las masas de las placas son iguales, encontrar la relación entre la energía potencial de las placas. 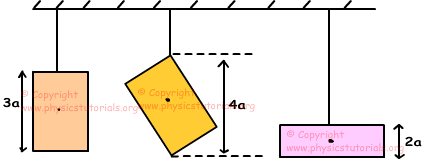Las masas de las placas son iguales, pero el centro de masas son diferentes.

EP₁=m.g.3a/2

EP₂=m.g.2a

EP₃=m.g.a

EP₂ >EP₁ > EP₃

5. A continuación el sistema está en equilibrio. Si la energía potencial de los objetos A y B son iguales, determine la masa del objeto A en términos de G. (Rod es homogénea y el peso de la misma es G.) Desde la barra es homogénea que puede tomar el peso de la misma en el centro. Igualdad de energías potenciales;

GA.4h=GB.h

GB=4GA.

Momento del sistema;

GA.3+G.1=GB.1

3GA+G=4GA

GA=G