Propiedades De La Materia Del Examen 1 Y Soluciones A Los Problemas
1. Tres tubos de diferentes están llenos de líquido que d₁ misma densidad. Si el resto de los tubos se llenan con otro líquido que tenga la densidad d₂, encontrar la relación entre las densidades de los líquidos en los tubos. (d₂>d₁)
Alturas de tres tubos son iguales, por lo tanto líquidos mezclados en los tubos tienen el mismo volumen. Las densidades de los líquidos se convierten;
d₁=d₂=d₃
2. Masa vs volumen gráfico de dos líquidos se dan a continuación. Si tomamos 160 gramos de agua X y 40 cm³ de agua Y, hallar la densidad de la mezcla homogénea.
Usando el gráfico dado anteriormente;
dx=80/20=4g/cm³
dy=40/20=2g/cm³
dmezcla=(mx+my)/(Vx+Vy)
dmezcla=(mx+Vy.dy)/mx/dx+Vy
dmezcla=(160+40.2)/160/4+40
dmezcla=3g/cm³
3. Nosotros mezclamos dos líquidos diferentes que tienen volúmenes iguales y d₁ = densidad 0,8 g/cm3 y d₂ = d. Si la densidad final de la mezcla es de 1,2 g/cm³, hallar la densidad de líquidos de segunda.
Si el volumen de asuntos son iguales que utilizamos la siguiente fórmula para encontrar la densidad de la mezcla;
dmezcla=(d₁+d₂)/2
1,2=(0,8+d)/2
2,4-0,8=d
d=1,6g/cm³
4. Las tasas de flujo de dos grifo son iguales y los líquidos tienen una densidad en 3D y d. Estas dos fases de llenar el tanque de la mitad de la muestra en la imagen a continuación y el resto del tanque es llenado por el grifo con la densidad del líquido d. Dibuje la densidad vs gráfico en tiempo de líquido en el tanque.
Dado que los caudales de los dos grifos son iguales, la densidad de la mezcla en la primera mitad es;
dmezcla1=3d+d/2=2d
Resto del tanque es llenado por el grifo con la densidad del líquido d. Por lo tanto, la densidad final de la mezcla se vuelve;
dmezcla2=2d+d/2=1,5d
Gráfico de densidad en función del tiempo de mezcla;
5. Un prisma hecho de materia con una densidad 5 g/cm³, tiene una masa de 600g. Encuentre el volumen del espacio en el interior del prisma.
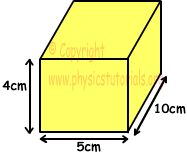Volumen exterior del prisma;
Vexterior=4.5.10=200cm³
Volumen de la materia utilizada para prisma=600/5=120cm³
Por lo tanto;
Volumen del espacio en el interior del prisma es=200-120=80cm³