Magnetismo Examen 1 Y Soluciones A Los Problemas

1. Encuentra las fuerzas ejercidas por los polos de los imanes S se indican a continuación. Magnetism F=k.M₁.M₂/r²=(10⁻⁷.10⁻⁴.10⁻³)/(0,6)²

F=10⁻¹⁴/(36.10⁻²)

F=10⁻¹²/36

2. Encontrar el campo magnético resultante en el punto O, producida por I₁, I₂ y I₃. Magnetism Magnitudes de los campos magnéticos;

B₁=2k.6/0,1=12.10⁻⁷/10⁻¹=12.10⁻⁶ N/Amps.m

B₂=2k.4/0,1=8.10⁻⁷/10⁻¹=8.10⁻⁶ N/Amps.m

B₃=2k.8/0,1=16.10⁻⁷/10⁻¹=16.10⁻⁶ N/Amps.m Magnetism Bresultant=B₁+B₂+B₃

Bresultant=√(12.10⁻⁶-16.10⁻⁶)²+(8.10⁻⁶)²

Bresultant=4√5.10⁻⁶ N/Amps.m

3. Cables A, B y C se indican a continuación. Determinar el campo magnético de A, B y C en los puntos X e Y. Magnetism Direcciones de los campos magnéticos en el punto X se encuentran utilizando la regla de la mano derecha.

BA: exterior

BB:interior

BC:interior

BX=BB+BC-BA

BX=2k.3I/3d+2k.I/d-2k.I/d=2k.I/d

Direcciones de los campos magnéticos en el punto Y lo son;

BA: interior

BB:interior

BC:exterior

BY=BA+BB-BC

BY=2k.I/d+2k.3I/d-2k.I/d=2k.3I/d

Relación de los campos magnéticos;

BX/BY=2k.I/d/2k.3I/d=1/3

4. Número de bucles de solenoide con N y la superficie A se muestra en la imagen a continuación. Si cambiamos la posición del solenoide, como se muestra en la imagen siguiente, encontrar la ecuación utilizada para encontrar fem inducida de solenoide. Magnetism inducida emf=ε=-(∆Φ)/(∆t).N

Cambio en el flujo;

∆Φ=Φ₂-Φ₁

Φ₁=0, ya que el área de sección transversal del solenoide y líneas de campo magnético son paralelos entre sí.

Φ₂=B.A

∆Φ=B.A-0=B.A

ε=-B.A.N/t

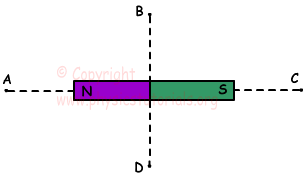
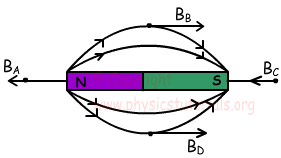
5. Dibuje las instrucciones de las líneas del campo magnético en el punto A, B, C y D en la imagen a continuación. Magnetism Direcciones de las líneas de campo magnético se han extraído de polo N a S poste como se muestra en la imagen a continuación. Magnetism