Impulso, Momento Exámen 1 Y Soluciones

1. Un objeto que viaja con una velocidad de 4 m s / hacia el este. Entonces, la dirección del movimiento y la magnitud de la velocidad se cambian. Cuadro que se presenta a continuación muestra las direcciones y magnitudes de las velocidades. Buscar el impulso dado a este objeto. I=F.Δt=Δp=m.ΔV

donde ΔV=V₂-V₁=-3-4=-7m/s

I=m.ΔV=3.(-7)=-21kg.m/s

2. Balón tras 4 kg de masa y la velocidad de 8 m/s viaja hacia el este. Impulso dado en el punto O, lo hace cambiar de dirección hacia el norte con una velocidad de 6 m/s. Buscar el impulso y el cambio en el momento. 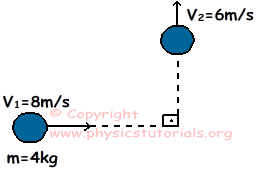Vectores cantidad de momento inicial y final de la pelota se muestran en la figura siguiente. P₁=m.V₁=4kg.8m/s=32kg.m/s

P₂=m.V₂=4kg.6m/s=24kg.m/s

ΔP=P₂+P₁ (Además vector)

ΔP²=P₂²+P₁²=m²(v₂²+v₁²)

ΔP₂=16.100

ΔP=40kg.m/s

Impulso = cambio en el momento

I=ΔP=40kg.m/s

3. Encontrar el impulso y la fuerza que hacen que el cambio 12m / s en la velocidad del objeto que tiene 16 kg de masa en 4 s.

F.Δt=ΔP=m.ΔV

F.4s=16kg.12m/s

F=48N

F.Δt=Impulso=192kg.m/s

4. Fuerza aplicada vs gráfico en tiempo de objeto se presenta a continuación. Buscar el impulso del objeto entre 0 y 10 segundos. El área bajo la gráfica de la fuerza frente al tiempo nos da impulso.

F.Δt=20.2/2+20.(6-2)+20.(10-6)/2

F.Δt=140kg.m/s

5. Un balón que golpea la pared de masa 500 g con 10 m/s de velocidad. La pared se aplica la fuerza 4000 N a la bola y se convierte de nuevo con 8 m/s de velocidad. Encontrar el momento de la pelota de la pared de contacto.

F.Δt=ΔP=m.ΔV=m.(V₂-V₁)

-4000.Δt=0,5kg.(8-10)

Δt=0,00025s