Temperatura De Calor Y Los Exámen 1 De Expansión Térmica Y Problema Soluciones

1. Dos termómetro X muestra el punto de ebullición del agua 220X y el punto de congelación del agua y 20X Y muestra el punto de ebullición del agua 120 Y y el punto de congelación del agua-40Y. Si el termómetro muestra X 100X, encontrar el valor que el termómetro Y muestra. (X-20)/200=(Y-(-40))/160

(X-20)/20=(Y+40)/16

Y=24⁰Y

2. Dos cuestiones han capacidades de calor específico c y 2c. Si le damos Q y el calor 4Q a estos asuntos, los cambios en las temperaturas de ellos se hacen iguales. Si el asunto tiene una masa m, determine la masa de B la materia en términos de m.

Calor ganado, perdido por la materia se encuentra con la siguiente fórmula;

Q=m.c.ΔT

Calor ganado por A y B;

Q=mA.c.ΔT

4Q=mB.2c.ΔT

mB=2mA

mB=2m

3. Cuestiones A y B tienen masas iguales. Encontrar la relación de cA / cB. Q=m.c.ΔT

30=m.cA.(10-0)

30=m.cB(20-0)

cA/cB=2

4. Tabla anterior muestra la longitud inicial, los cambios en las temperaturas y los cambios en la longitud de tres barras. Averiguar si estas barras están hechas de materia misma o no.

ΔL=L₀.α.ΔT

αA=ΔL/2L.ΔT

αB=3.ΔL/3L.2ΔT

αC=ΔL/4L.ΔT

αA=αB>αC

Por lo tanto, A y B puede ser la materia misma, pero C es diferente de ellos.

5. Tres cilindros hechos de la materia misma y a la misma temperatura, se colocan sobre una plataforma. Misma cantidad de calor que a los cilindros de hacer la misma cantidad de cambio en su temperatura. Encontrar la relación entre los cambios en las longitudes de estos cilindros. 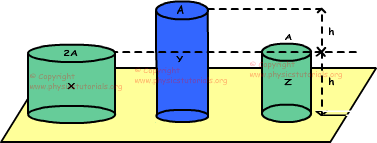Si decimos que el volumen de X es V, entonces el volumen de Y es también V y Z es V / 2. Existe una relación lineal entre el volumen y la masa, se utiliza esta relación en la solución del problema.

Q=m.c.ΔTX, ΔTX=T

Q=m.c.ΔTY, ΔTY=T

Q=m/2.c.ΔTZ, ΔTZ=2T

Los cambios en la longitud de los cilindros;

ΔLX=h.α.T=ΔL

ΔLY=2h.α.T=2ΔL

ΔLZ=h.α.2T=2ΔL

ΔLY=ΔLZ>ΔLX