Cinemática Examen 4 Y Soluciones De Problemas

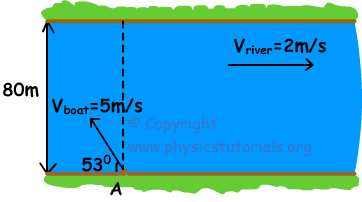1. Mira las fotos dado y encontrar que uno de los vectores dados en la segunda figura es la velocidad relativa de A respecto a B. Kinematics Ya que el observador es la B, nos encontramos con la velocidad relativa de A respecto a B con la siguiente fórmula; VAB = VA-VB Usando las propiedades de vector Además nos encontramos con la velocidad relativa como figura a continuación. Kinematics 2. La velocidad del río con respecto a la tierra es de 2m / s hacia el este. Anchura del río es de 80m. Un barco inicia su movimiento en este río en el punto A con una velocidad de muestra en la figura siguiente. Encontrar el tiempo del movimiento y la distancia horizontal entre el punto de llegada y el punto A. Kinematics Componentes de la velocidad de barco; Vx=5.cos530=-3m/s hacia el oeste Vy=5.sin530=4m/s hacia el norte

Tiempo para pasar el río es; t=X/V=80m/4m/s=20s

Velocidad resultante en horizontal; VR=VX+Vriver VR=-3+2=-1m/s to the west

Distancia tomada en horizontal; X=V.t X=1m/s.20s=20m

3. Un barco por el río en un río que viaja a velocidad constante, la distancia 120m del punto A al B en 20 s, y se vuelve de B a A en 12 s. Si la velocidad del río es igual a cero, encontrar el tiempo de este viaje. 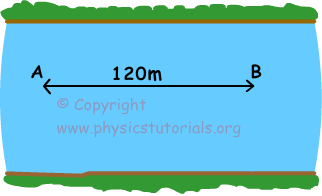Kinematics Desde los tiempos de viaje de B a A es más largo que el tiempo de viaje de A a B, la dirección de la velocidad del río se encuentra al oeste. Velocidad del río con respecto a la tierra es Vriver, y la velocidad del barco con respecto al río es Vboatriver. Velocidad del barco con respecto a tierra cuando se viaja de A a B se convierte;

Vb=Vboterío-Vrío

y cuando se viaja de B a A;

Vb=Vboterío+Vrío

Podemos encontrar la velocidad utilizando la siguiente fórmula;

1.Vboterío-Vrío=120/20=6m/s y 2.Vboterío+Vrío=120/12=10m/s

La resolución de ecuaciones 1. y 2. nos encontramos con la velocidad del río y el barco.

Vboterío=8m/s and Vrío=2m/s

Si la velocidad del río es igual a cero, barco distancia que viaja 240 millones en;

240=8m/s.t

t=30s

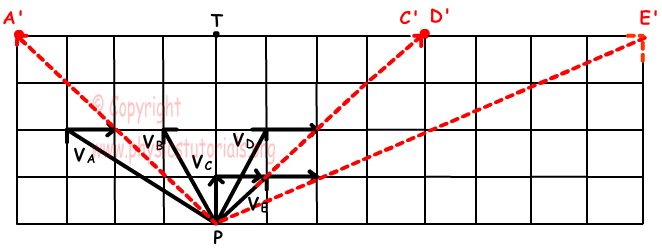
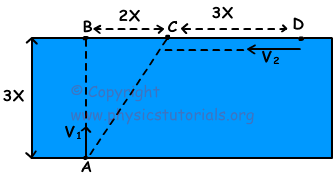4. Cinco nadadores empiezan a nadar desde el punto P. Si el nadador B pasa el río y llega al otro lado del río en el punto T, encontrar los puntos de salida de otros nadadores desde el río. Kinematics Desde el nadador B llega al otro lado del río en el punto T, la velocidad del nadador B debe ser en la dirección del PT. Nos encontramos con la velocidad del río como una unidad hacia el este. Cuadro que se presenta a continuación muestra los puntos de salida de otros nadadores de río. Kinematics 5. Dos nadadores empiezan a nadar al mismo tiempo, como se muestra en la imagen siguiente. Si cumplen con el punto C, encontrar la relación de sus velocidades con respecto al agua. Kinematics Si no hay velocidad del río, swimmer₁ alcanza el punto B, y swimmer₂ alcanza el punto B, sin embargo, la velocidad del río les hace llegar al punto C. En otras palabras, que la velocidad V₁ swimmer₁ toma distancia de 3X y swimmer₂ V₂ con la velocidad de toma distancia de 5 veces durante el mismo tiempo. Por lo tanto;

V₁/V₂=3/5