Cinemática Examen 2 Y Soluciones De Problemas

1. Un objeto se deja caer desde 320 metros de altura. Encontrar el tiempo de movimiento y la velocidad al chocar contra el suelo.(g=10m/s²)

h=1/2.g.t² , v=g.t

h=320m

g=10m/s²

320=1/2.10.t²

t=8s.

v=g.t=10.8=80m/s

2. Un objeto se encuentre libre y que toma distancia de 60m en los últimos dos segundos de su movimiento. Encontrar la altura que se ha caído.(g=10m/s²) t es el tiempo de movimiento

h=1/2.g.t²

h₁=1/2.g.t₁²

poner t₁=t-2 y h-h₁=60 en la ecuación,

1/2.g.t²-1/2.g.t₁²=60

5t²-5(t²-4t+4)=60

t=4s

h=1/2.g.t²=1/2.10.4²=80m

3. Un objeto se deja caer desde la altura de 144m y lo hace el movimiento de caída libre. Distancia que recorre y el tiempo del movimiento se dan en la siguiente imagen. Encontrar la distancia entre los puntos B, C. Podemos dibujar el gráfico de velocidad de tiempo de un objeto y el área bajo la gráfica nos da la posición del objeto. 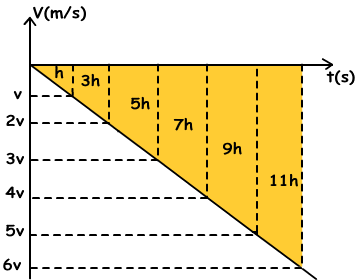Como se puede ver en el gráfico de tiempo la velocidad, la distancia que viaja la 5h objeto durante 2t-3t, que es la distancia entre los puntos B y C.

Todos distancia recorrida es 36h

144m=36h

h=4m

Distancia entre B-C=5h=5.4m=20m

4. Un globo de aire caliente que se eleva la velocidad inicial V₀. Piedra dejada caer desde el globo, cuando es de 135 m de altura, cae al suelo después de las 9 s. Calcular la velocidad del balón. -h=V₀.t(vuelo)-1/2.g.t(vuelo)²

-135=v₀.9-1/2.10.(9)²

-135=9V₀-405

9V₀=270

V₀=30m/s

5. Mira la foto a continuación. K es el movimiento de objetos en caída libre y B objeto lanzado hacia arriba, al mismo tiempo. Chocan después de 2s. Encontrar la velocidad inicial del objeto B.(g=10m/s²) Objeto A es el movimiento de caída libre

hA=1/2.10.2²=20m

hL=V₀.t-1/2.g.t²

hL=V₀.2-1/2.10.2²

hL=2V₀-20

hK+hL=80m

20m+hL=80m

2V₀-20=60m

V₀=40m/s