Capacitors in Series and Parallel
Systems including capacitors more than one has equivalent capacitance. Capacitors can be connected to each other in two ways. They can be connected in series and in parallel. We will see capacitors in parallel first.
In this circuit capacitors are connected in parallel.
Because, left hand sides of the capacitors are connected to the potential a, and right hand sides of the capacitors are connected to the potential b. In other words we can say that each capacitor has same potential difference. We find the charge of each capacitor as;
Q₁=C₁.V
Q₂=C₂.V
Q₃=C₃.V
Total charge of the system is found by adding up each charge.
Qtotal=Ceq.V
Qtotal= Q₁+Q₂+Q₃=C₁.V+C₂.V+C₃.V=V.(C₁+C₂+C₃)=Ceq
Ceq=C₁+C₂+C₃
As you can see, we found the equivalent capacitance of the system as C₁+C₂+C₃
Now we will see the capacitors in series;
In capacitors in series, each capacitor has same charge flow from battery. In this circuit, +Q charge flows from the positive part of the battery to the left plate of the first capacitor and it attracts –Q charge on the right plate, with the same idea, -Q charge flows from the battery to the right plate of the third capacitor and it attracts +Q on the left plate. Other capacitors are also charged with same way. To sum up we can say that each capacitor has same charge with batter.
C₁.V₁=Q
C₂.V₂=Q , V=V₁+V₂+V₃ and Q=Ceq.V
C₃.V₃=Q
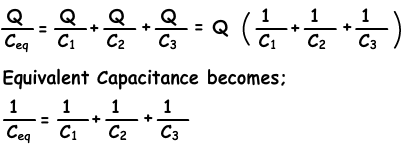Example: Calculate the equivalent capacitance between the points a and b.
Example: In the circuit given below, C₁=60µF, C₂=20 µF, C₃=9 µF and C₄=12 µF. If the potential difference between points a an b Vab= 120V find the charge of the second capacitor.
