Electric Current Cheat Sheet
Electric Battery
Electric battery is a device that converts chemical energy to the electrical energy.
Electric Current and Flow of Charge
If we connect the conductor to a battery, potential difference between the ends of the conductor occurs. This potential difference creates an electric field towards to the positive end of the conductor to the negative end. Free charges inside this electric field are exerted a force F=q.E in this field. Under the effects of this force electrical charges starts to flow. This flow of charge is called electric current.
Average current I is found with the following formula;
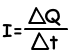Where; I is the current, Q is the charge and t is the time
The unit of electric current is Coulomb per second, and we give specific name Ampere (A).
Ohm’s Law Resistance and Resistors
Resistance is the difficulty applied by the conductor to the current flowing through it. Each material has different resistance. We show resistance with R and unit of it is ohm (Ω).
1 Ω=resistance of the conductor when 1 A current flows under the 1 V potential difference. Resistance is represented with the following picture in circuits;
We can write our formula with the explanation given above as;
Ohm’s Law
Ohm’s law gives the relation between voltage, current and resistance
Combination of Resistors
Resistors can be combined in two ways; series and parallel. Combination of more than one resistor is called equivalent resistor. We first look at the resistors in series;
Resistors in Series
a. In this types of circuit, amount of currents passing through the resistors are equal and this current comes from the battery.
i=i₁=i₂=i₃
b. Sum of the potential differences of each resistor is equal to total potential difference of the circuit or potential difference between the ends of battery.
V=V₁+V₂+V₃
We substitute these values into the ohm’s law and get equivalent resistance;
Req=R₁+R₂+R₃
Resistors in Parallel
a. Sum of the currents in each branch is equal to the current coming from battery.
it=i₁+i₂+i₃
b. Since the two ends of each resistor are connected to the same points, potential differences of each resistor are equal.
V=V₁=V₂=V₃
Substituting these values into the ohm’s law, we get the equivalent resistance equation as;
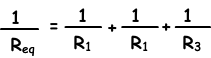Common Electric Circuits and Combination of Batteries
1. Batteries: Device which supplies energy to the circuit is called battery. We show it in the circuit as;
EMF: It is the energy given by the battery to the unit charge when it passes from one end to the other end of the battery. If the battery gives W joule to a charge Q, then;
ε=W joule
We can say that, if the EMF of the closed circuit is known then EMF is directly proportional to the charge in the circuit.
W=ε.Q where Q=i.t
W=ε.i.t
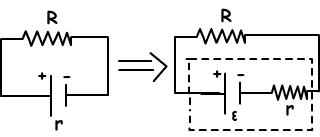
Batteries in Series: In this type of combination + end of the battery is connected to the – end of the other battery. Pictures given below show the examples of this type of combination.
Total EMF of the circuit is;
εeq=ε₁+ε₂+ε₃+…+εn
Batteries in Parallel: In this type of circuits, batteries must be identical. Picture given below shows the example of batteries in parallel;
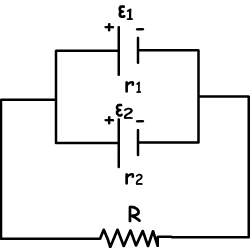Total EMF of the circuit;
εeq=ε₁=ε₂=ε
Total internal resistance of the batteries is;
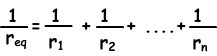Diodes
Diodes are kinds of device that allow current flow only in one direction in circuits. Thus, only half of the cycles of alternating current can pass from the diodes.
Electric Power and Energy
E=V.i.t
Where, E is the heat, V is the potential difference of the battery and t is the time. If we substitute i.R in terms of V then we find following energy equation.
E=i².R.t=V²/R.t
Electric Power
It is the energy emitted in a unit of time by the conductor.
Power=Electric Energy/time
P=V.i.t/t
P=i.V or if we put i.R in terms of V (ohm’s law)
P=i².R=V²/R
Finding the Potential Difference between the Two Points in Circuits with Examples
Potential difference between two points in circuit is the energy lost by the charge in being transferred from one point to another. For example, potential difference between A and B is found with following formula;
VAB=VB-VA=∑ε-∑i.R